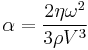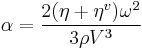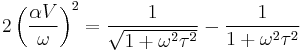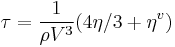Stokes' law (sound attenuation)

Stokes derived a law for the attenuation of sound in a Newtonian fluid[1].

According to this law attenuation of sound α is proportional to the dynamic viscosity η, square of the sound frequency ω, and reciprocally proportional to the fluid density ρ and cubic power of sound speed V

\alpha = \frac{2 \eta\omega^2}{3\rho V^3}

Attenuation is expressed in neper per meter in this equation. The author of this law is the same famous George Gabriel Stokes who derived the well-known Stokes' law for the friction force in fluids. It is 160 years old. This remarkable law does not contain unknown or unmeasurable parameters.

It is convenient to convert attenuation into other units, by normalizing attenuation with respect to frequency, because the attenuation typically increases rapidly with frequency. These new units make more adequate presentation of attenuation within a wide frequency range. It is seen that attenuation of the Newtonian fluid, presented in these units, becomes a linear function of frequency.

There has been substantial theoretical development in this field since Stokes’ pioneering work. It has brought one important correction to the Stokes law. It turns out that in addition to the dynamic viscosity the parameter of volume viscosity ηv also affects the total attenuation according to the following relationship:

\alpha = \frac{2 (\eta%2B\eta^v)\omega^2}{3\rho V^3}

The parameter volume viscosity is surprisingly little known despite its fundamental role for fluid dynamics at high frequencies. This parameter appears in Navier-Stokes equation if it is written for compressible fluid, as described in the most books on general hydrodynamics [2], [3], and the acoustics [4], [5].

This volume viscosity coefficient becomes important only for such effects where fluid compressibility is essential and, importantly, ultrasound propagation is one such effect. Indeed, many rheological texts just assume the fluid to be incompressible and the volume viscosity therefore plays no role.

The only values for the volume viscosity of simple Newtonian fluids known to us come from the old Litovitz and Davis review [6]. They report a volume viscosity of water at 15 Co equals 3.09 centipoise

More recent studies have established that Stokes's law is actually a low frequency asymptotic of the more general relationship that describes sound attenuation at very high frequencies:
2\left(\frac{\alpha V}{\omega}\right)^2 = \frac{1}{\sqrt{1%2B\omega^2 \tau^2 }}-\frac{1}{1%2B\omega^2 \tau^2}

where relaxation time τ equals:

\tau = \frac{1}{\rho V^3}(4 \eta/3 %2B \eta^v)

Corresponding relaxation frequency is about 1000 GHz. It is extremely high. For all practical purposes of describing sound attenuation in Newtonian fluids Stokes' law is clearly sufficient.

References

  1. ^ Stokes, G.G. "On the theories of the internal friction in fluids in motion, and of the equilibrium and motion of elastic solids", Transaction of the Cambridge Philosophical Society, vol.8, 22, pp. 287-342 (1845
  2. ^ Happel, J. and Brenner , H. "Low Reynolds number hydrodynamics", Prentice-Hall, (1965)
  3. ^ Landau, L.D. and Lifshitz, E.M. "Fluid mechanics", Pergamon Press,(1959)
  4. ^ Morse, P.M. and Ingard, K.U. "Theoretical Acoustics", Princeton University Press(1986)
  5. ^ Dukhin, A.S. and Goetz, P.J. "Ultrasound for characterizing colloids", Elsevier, (2002)
  6. ^ Litovitz, T.A. and Davis, C.M. In "Physical Acoustics", Ed. W.P.Mason, vol. 2, chapter 5, Academic Press, NY, (1964)